本章主要内容：

　　l 计量资料的统计描述，主要包括资料的位置指标与离散指标

　　l 计数资料的统计描述，主要包括率、构成比、相对比等

　　2.1 计量资料的统计描述

　　2.1.1 频数表(frequency table)

　　2.1.1.1 频数表的概念及制作

　　制作频数表是整理计量资料最常用的方法，现以实例介绍频数表的制作方法。

　　例2.1 1999年，某饮料公司以街访的方式对100名消费者进行了500ml瓶装可乐的价格进行了测试，关于问题‘您认为最合适的价格应该是多少?’的回答，资料如下(单位：元)：

 

　　(1) 寻找资料中的最大值、最小值，计算极差

　　本例最大值M=3.22

　　最小值m=1.71

　　最大值与最小值之差称为极差，常用R表示

　　R=M-m=3.22-1.71=1.51

　　(2) 确定组距、组段数

　　频数表一般设10~15个组段，观察值少时可相对少些，组段数n多时可多些，

　　组段数为n，组距h，极差R有如下关系：

　　本例共100个数据，可分10个组段，n=10，则h=1.51/10=0.151»0.15

　　各个组段应界限分明，每个组段的起点称为‘下限’(low limit)，终点称为‘上限’(upper limit)，各个组段从本组段的‘下限’开始，不包括本组段的‘上限’;第一组应包含资料中的最小观测值，最后一组应包含资料中的最大值;第一组从最小值开始，或一个符合日常习惯的数值开始，如，本例可从1.70开始，第一组段为1.70~，第二组段为：1.85~，依次类推，最后一个组段为，见表2.1第一列

　　(3) 扫描样本值，划计后获得频数

　　划记的方法是，按行(或者按列)，从第一个原始数据开始，逐一判断该数据属于哪一个组段，然后在相应的组段作一个记号，本书采用‘*’作为记号。如：第一个数据‘2.67’，属于第七个组段‘2.60~’，在相应组段划‘*’，第二个数据2.88，属于第八个组段‘2.75’，在相应组段‘2.75~’作记号‘*’，依次类推，直至将所有的数据‘读完’，得到表2.1的第二列，划记完成，清点第二列每组段的‘*’数，得到相应组段的频数，记入第三列，第一、第三列即为做的频数表。

　　表2.1 100名被访者关于500ml可乐认可价格的频数表

　　从频数表的制作过程可见，频数表是反映原始数据在每一个组段数据出现频次的表格。

　　2.1.1.2 频数表的用途

　　(1) 从表2.1可见，数据向组段‘2.45~’集中，以该组段周围的原始数据居多，原始资料向某一数据段(或某一数据)周围的集中、靠拢的特点，在统计学上称为资料的集中趋势。

　　(2) 从表2.1还可看到，原始数据有大有小，差异较大，最大值与最小值相差1.51，从1.71到3.22，从中央向两侧逐渐减少，而这种从小到大的分布特点，在统计学上称为离散趋势。

　　(3) 从表2.1还可看到，第一组段有2个数据，最后一个组段有1个数据，最小、与最大清楚地摆在面前，有利于我们去重点监督。

　　由此可见，频数表至少有如下用途：

　　1)揭示资料的分布特征和分布类型

　　2)便于发现某些特大、特小的可疑值

　　3)便于指标计算和统计分析

　　2.1.1.3 频数分布的常见类型

　　(1) 对称分布 表2.1是频数表最常见的类型，资料集中在某一数据的周围，左右两侧对称，资料的这种分布，称为对称分布。

　　(2) 偏态分布 表2.2，资料偏向价格较大的一侧，表2.3，资料偏向价格较小的一侧，资料的这种分布称为偏态分布。其中，向大的一侧偏向，称为正偏态分布;向小的一侧偏向，称为负偏态分布。

　　表2.2 某资料的频数表

　　表2.3 某资料的频数表

　　2.1.2 资料的集中趋势

　　平均数(average)：统计应用中最重要的一个指标体系，常用于描述一组变量值的集中位置，代表平均水平。或者说它是集中位置的特征值。

　　平均数的计算和应用要求资料必须具备同质的基础，否则，计算的指标没有实际意义，如：把电视价格与冰箱的价格放在一起相加，没有任何意义。

　　常用的平均数包括：均数、几何均数、中位数、众数等，下面一一介绍。

　　2.1.2.1 均数(mean)

　　均数是算术平均数的简称，其计算是将观测值相加，然后除以资料的个数，是最常用的平均数的计算方法，反映一组观测值在数量上的平均水平。

　　(1) 计算公式

　　假定观测值为x1、x2、 … xn，公式为

                                                             　(2.1)

　　如：5家商店21英寸的彩电的销售价格分别为：1038、995、1120、1080、1088，则五家商店的平均价格(均数)为

　　由于公式(2.1)按照算术平均数的定义直接计算，公式所表达的含义也比较清楚，故称之为直接法。当资料中相同的观测值较多时，可将相同观测值的个数，即频数f，乘以该观测值X，以代替该观测值逐个相加，如：资料中有5家商店价格均为1088，则在计算时，不必：1088+1088+1088+1088+1088=5440，而直接用5乘1088即可：1088´5=5440，频数5在统计学上也称为权重，由此得到计算均数的‘加权法’公式：

                                                                      (2.2)

　　例：见表2.1，计算100名消费者对500ml瓶装可乐的平均价格

　　计算表2.1中每组的组中值，计算方法是：将每组的上限与下限相加，然后除以2，如：第一组，下限为1.70，上限为1.85，组中值为(1.70+1.85)/2=1.775，结果见表中第三列。组中值是属于该组段的原始数据的代表，如，第一组段有2个数据，我们可以认为，这两个观测数据均为1.775，然后计算每一组段的观测数据的代数和，即组中值乘以相应频数，得第四列数据，将第四列相加，得所有观测值的代数和，由公式(2.2)计算出均数为：2.50(元)

　　表2.4 100名消费者对500ml瓶装可乐的平均认可价格的计算

　　均数的两个重要特性：

　　各离均差的代数和等于0，即

 

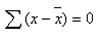
　　离均差为每个观测值与均数的差值，即： ，反映每一个个体观测值相对与均数的离散情况。如：第一家商店彩电价格为1038元，相对与平均价格1064.2元，离均差为：1038-1064.2= -26.2，既，第一家商店比平均价格低26.2元。

　　(2)离均差的平方和小于各观测值与任何数之差的平方和。

　　应用范围：均数反映全部观测值的平均水平，因而应用非常广泛。但它最适用于对称分布资料，尤其正态分布资料。

　　2.1.2.2 几何均数(geometric)

　　计算方法：

　

　　(1)直接法：

　　(2)加权法：

　　2.1.2.3 中位数(median)

　　将一组观察值按从小到大顺序排列，位次居中的观察值称为中位数。全部观察值中，大于和小于中位数的观察值个数相等，常用M表示。

　　计算公式：资料按从小到大的顺序排序x1£x2£ … £xn

　　当n为奇数时，

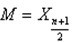
　　当n为偶数时，

　　如：调查了5家工厂的职工数，分别为：15，30，61，180，500，中位数M=61人;若调查了6家，分别为：15，30，61，100，180，500，则中位数M=(61+100)/2=80.5(人)

　　2.1.2.4 众数(mode)

　　全部观察值中，出现频率最多的那个观察值称为众数。

　　在推出400ml洗发水前，某企业举行了一场有关其价格定位的座谈会，8位专家中有5位认为该产品定价应为35元，则8个调查数据中35出现的频次最高，因此其众数为：35元。

　　2.1.2.5 百分位数(percentile)

　　百分位数是位置指标，以Px表示。Px将总体分成两部分，理论上有x%的观察值比它小，(100-x)%的观察值比它大，中位数是特殊的百分位数。

　　利用频数表计算百分位数的公式为：

　　式中fx为Px所在组段的频数，i为该组段的组距，L为其下限，SfL为小于L的个组段的累计频数。

　　例，某资料的频数分布见表2.5，首先计算频率，样本含量为114，每一组段的频数除以样本含量得该组段的频率，见第三列，每一组段的频数加上前面各组段的频数，得该组段的累计频数，见第四列。

　　(1) 计算百分之25位数P25，从表2.5第五列可见，从第一组段至第二组段，即从1.70至2.00(不包括2.00)，共含有样本总数21.93%的个体，从第一组至第三组，共含有总数38.6%的个体，根据百分位数的定义，P25应在第三组段的范围内，因此，L=2.00，i=0.15，fx=19，SfL=21.93 又n=114，x%=25%

　　由公式，

　　同理，可计算P50，即中位数M及P75

　　表2.5 百分位数的计算

　　2.1.3 离散趋势

　　2.1.3.1 极差(range，简记为R)

　　一组资料中，最大值与最小值之差称为极差，常用R表示。用M表示最大值，m表示最小值，计算公式为：

　　R=M-m

　　如：某资料，最大值M=3.22，最小值m=1.71，则极差R=3.22 - 1.71=1.51

　　优点：利用极差来说明资料变异度的大小，简单明了，在资料描述时经常用到。

　　缺点：除最大、最小值外，不能反映其它数据的变异情况;不够稳定，当样本量相差悬殊时，不宜进行样本间变异度的比较。

　　2.1.3.2 四分位数间距(quartile,Q)

　　P25位数，表示全部观测值中，四分之一的观测值比它小;P75，表示四分之一的观测值比它大，因而称P25、P75为四分位数，其中P25为下四分位数，常用QL表示，P75为上百分位数，常用QU表示

　　Q=QU-QL=P75 - P25

　　如：前面的例题中，QL P25=2.03，QU =P75=2.40，则：

　　Q=QU-QL=2.40-2.03=1.3

　　优点、缺点同极差类似，四分位数间距比极差稳定。

　　2.1.3.3 方差(variance)

　　用极差或四分位数间距来描述资料的变异情况，仅用到资料中的两个数据，不能反映其他资料的情况，为反映资料中的所有个体对变异度的影响，研究中首先想到了离均差这一指标。以均数为m的总体为例，离均差之和即S(x-m)=0，自然想到将每一个观测值的离均差平方后再相加(称为离均差平方和，英文：sum of squares，简记为SS或lxx)，即计算S(x-m)2，由于其大小还与个体的数目有关，故将其除以变量值的个数N后，得到描述总体变异的指标---方差，公式为：

                               　(2.09)

　　公式(2.09)称为总体方差，对样本而言，数理统计证明，方差为：

                                          　(2.10)

　　加权公式为：

                                    　(2.11)

　　公式(2.10)称为样本方差，其中n-1称为自由度(degree of freedom)。

　　例，计算例2.1资料的标准差

　　由表2.1，åfx=250.85，åfx2=640.19 n=åf=100，代入公式(2.11)

　　关于方差的分子部分，即离均差平方和，还可以写成如下表达式：

            　(2.12)

　　2.1.3.4 标准差(standard deviation)

　　方差的单位是原单位的平方，将之开方后，即得常用于描述资料变异度的指标—标准差，总体标准差用s，样本用S表示，计算公式分别为

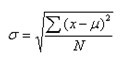                        　(2.13)

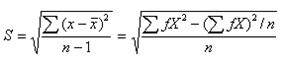                       　(2.14)

　　例2.1资料的标准差S为

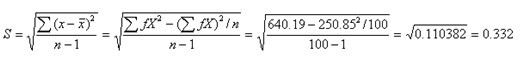
　　2.1.3.5 变异系数(coefficient of variation， 简记为CV)

　　变异系数亦称离散系数(coefficient of dispersion)，计算方法是将标准差S与均数 的比值，公式为：

　　应用：(1)度量衡不同的资料间变异度的比较

　　(2)均数相差悬殊的资料间的比较

　　2.2 分类资料的统计描述

　　2.2.1 常用相对数

　　2.2.1.1 率(rate)

　　率，又称频率指标，它说明某现象发生的频率或强度。

　　如：调查了100间零售店，其中35间有某产品出售，则该产品的铺货率为：

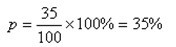
　　在有关洋酒的调查中，100名被访者中有85人知道马爹利，则马爹利的知名度为：

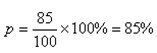
　　2.2.1.2 构成比(proportion)

　　构成比又称构成指标，它说明一事物内部各组成

　　部分所占的比重或分布，常以百分数表示。

　　如：调查了100名被访者，其中大专及以上学历者55人，则100名被访者中，大专及以上学历人员占的比例为：

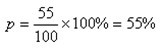
　　2.2.1.3 相对比(ratio)

　　相对比简称比，是两个相关指标之比，说明两个指标的相对水平。计算公式为：

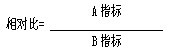
　　例：某品牌，在上海的知名度P1=0.65，在广州为P2=0.38，则该品牌的知名度上海相对与广州的相对比为：

　　广州相对与上海的相对比为：

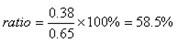
　　2.2.2 顾客满意表征指标(举例)

　　2.2.2.1 知晓度

　　知晓度=知晓人数/目标公众

　　2.2.2.2 知名度

　　(1)绝对知名度=认为企业或产品有名气的人数/目标公众

　　(2)相对知名度=认为企业或产品有名气的人数/知晓人数

　　2.2.2.3 美誉度

　　(1)绝对美誉度=褒扬者人数/目标公众

　　(2)相对美誉度=扬者人数/知晓人数

　　2.2.2.4 指名度

　　(1)绝对指名度=指名消费人数/目标公众

　　(2)相对指名度=指名消费人数/知晓人数

　　2.2.2.5 满意度

　　(1)绝对满意度=满意人数/目标公众

　　(2)相对满意度=满意人数/消费人数

　　2.2.3 动态数列及其分析指标

　　动态数列(dynamic series)是一系列按时间顺序排列起来的统计指标，包括绝对数、相对数或平均数，用以说明事物在时间上的变化和发展趋势。

　　现以实例介绍常用指标及其计算。

　　例，表3.1第(2)列给出了某公司1996~2000年净资产资料，现分析该公司该公司净资产逐年变化特点。

　　表3.1 某公司1996~2000年净资产资料分析表

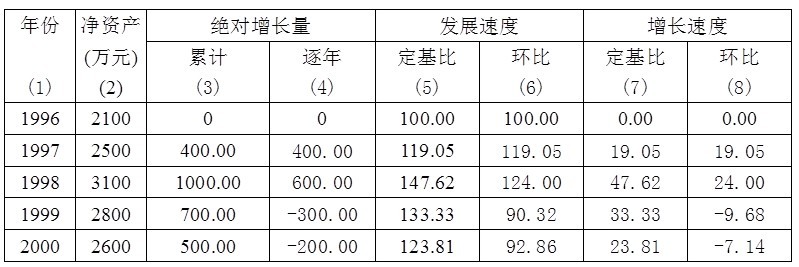
　　2.2.3.1 绝对增长量 说明事物在一定时期所增加的绝对的数量。绝对增长量常计算累计增长量、逐年增长量

　　(1) 累计增长量 以某年作为比较对象(基期)，其它年份与其相减，所得差值即为累计增长量。

　　本例以1996年数据作为基数，如：1998年净资产累计增长量为：2500-2100=400(万元)，其余年份的累计增长量见表3.1第(3)列。

　　(2) 逐年增长量 以下一年的数据与上一年的数据相减，所得差值即为逐年增长量。

　　本例以1997年净资产为2500万元，1998年为3100万元，1998年相对于1997年增长量为：3100-2500=600(万元)，其余年份的逐年增长量见表3.1第(4)列。

　　2.2.3.2 发展速度和增长速度

　　发展速度和增长速度常计算的指标是定基比、环比，增长速度=发展速度-1。

　　(1) 定基比，针对某一时间序列，统一用某个时间的指标作基数，以各时间的指标与之相比。反映变化的发展趋势。

　　如：以1996年净资产2100万元作为基数，1998年为3100万元，1998年相对于1996年的发展速度(定基比)为：

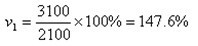
　　1998年对1996年增长速度(定基比)为：

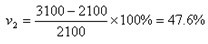
　　增长速度亦可由发展速度计算：

　　

　　其他时期的定基比见表3.1第(5)、(7)列。

　　(2) 环比，针对某一时间序列，以前一个时间的指标作基数，以相邻

　　的后一时间的指标与之相比。反映年度间的波动。

　　如：以1997年净资产2500万元作为基数，1998年为3100万元，1998年的环比发展速度为：

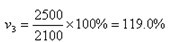
　　1998年的环比年增长速度为：

　　增长速度亦可由发展速度计算：

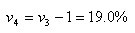
　　其他时期的环比指标见表3.1第(6)、(8)列。

　　2.2.3.3 平均发展速度/增长速度

　　平均发展速度/增长速度用于概括某一时期的速度的变化，计算公式如下：

　　假定基期数据为a0,各时期数据如下：a0、a1、a2、a3、…、an，an为第n的指标数据，则

　　平均发展速度

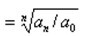
　　平均增长速度=平均发展速度-1

　　如：以1996年为基期，1999年净资产为2800万元，则a0=2100，n=3,a3=2800, 平均发展速度为：

　　平均增长速度=平均发展速度-1=110.1%-1=10.1%

　　自1996年至1999年，净资产平均发展速度为110.1%，平均增长速度为10.1%。

上一篇下一篇